Pierre Valenkoff ★• 30.12.24 04:59
> Законы устройства нашего мира таковы, что все распределены по Гауссиане
Самое смешное в этой истории, что в нашем мире по гауссиане не распределено ничто: она должна простираться от минус бесконечности до плюс бесконечности и при этом быть симметричной. А для мира живых она не годится даже как аппроксимация: рост, вес, зарплата и пр. даже близко не лежат к гауссиане.
А если речь идёт об интеллекте, там сумасшедший дом цирк следующего уровня: непонятно, в чём его мерять. Не в попугаях ли? Так что впариваемая бодяга с процентами - просто пи́здеж. Прошу прощения за ненормативную лексику, но нормативного синонима я не нашёл.
Kelavrik_0➦Pierre Valenkoff• 30.12.24 09:13
Вообще то нормальное распределение очень быстро выходит на вероятности 10^-100, которые просто не измерить. Потому о бесконечностях можно забыть.
Pierre Valenkoff ★➦Kelavrik_0• 30.12.24 19:04
Вероятности 10^-100 мало кого интересуют, но нормальное распределение, действительно, очень "острое", за что его любят математики. Но в реальных задачах распределение часто имеет "толстый хвост" - наблюдаемые значения отклоняются от центра гораздо чаще, чем предсказывает нормальное распределение.
Kelavrik_0➦Pierre Valenkoff• 30.12.24 19:29
Бывают и хвосты. Бывает и асимметрия. Всякое бывает. Это говорит о том, что условия для получения нормального распределения не соблюдались. Больше того, есть распределение Коши с бесконечной дисперсией. В мире много есть прикольного.
Pierre Valenkoff ★➦Kelavrik_0• 30.12.24 20:25
Ещё раз, медленно: прикол в том, что в реальности нормальное распределение встречается реже, чем в анекдотах. Именно потому что условия для получения нормального распределения никогда не соблюдаются.
Kelavrik_0➦Pierre Valenkoff• 30.12.24 21:59
Наоборот, они встречаются очень часто, просто просто в этом случае все спокойно вздыхают и отмечают факт как нормальный. Всего и надо, чтоб искомая величина была суммой случайных величин и чтоб дисперсия этих случайных величин была примерно одинаковой.
Pierre Valenkoff ★➦Kelavrik_0• 30.12.24 22:38
Если вы занимаетесь чем-нибудь простым и традиционным, например делаете болты, то их длина действительно хорошо описывается нормальным распределением.
Но оно встречается редко в современных задачах, например, в биомедицине. Вспоминая недавнюю эпидемию - какие величины там имели нормальное распределение? Частота случаев заболевания в городе - распределение Пуассона (закон редких событий) - его дисперсия равна его среднему. Испытание вакцины - распределение гипергеометрическое или χ2...
Но вы не горюйте: для получения нормального распределения из мн.др. используются преобразования, стабилизирующие дисперсию.
Kelavrik_0➦Pierre Valenkoff• 30.12.24 22:47
Постоянно в биомедицине и где угодно. Если мы оцениваем ошибку среднего. Так вот, среднее как раз и есть величина распределённая по нормальному закону.
Pierre Valenkoff ★➦Kelavrik_0• 30.12.24 23:53
Понятно. Продолжайте мерять болты средние по больнице.
Kelavrik_0➦Pierre Valenkoff• 31.12.24 00:37
Средние тоже важны. Кстати, именно болты не обязаны быть распределены по гаусу.
Pierre Valenkoff ★➦Kelavrik_0• 31.12.24 01:44
Если болты не распределены по Гауссу, что-то идёт не так! :-)
"Они хочут свою образованность показать и всегда говорят об непонятном" (С)
Если не приплетать сильно в математику и физику, да и не сильно ударяться в то, кто и как собирает статистику... То в целом очень простыми словами и по существу рассказано то, что люди в массе - стадо, а стадо затопчет того, кто выбивается из массы, или утащит за собой. Хоть в омут, хоть на бойню. Мысль не нова и справедлива, это, конечно, не откровение - но верно по существу и приятно подано по форме изложения. Спасибо и плюс.))
Некто Леша ★★★★★• 29.12.24 19:11
Эко заминусовали! Из этого следует, что минусеры - люди туповатые и обидчивые на эту тему :)
Andreiiiii➦Некто Леша• 29.12.24 22:24
Просто написана куча глупости. И про гауссиану в форме синусоиды, и про то, что люди распределены по этой "синусоиде".
Andreiiiii➦Irenbrau• 29.12.24 23:10
С гауссианой вообще бред, поскольку она заходит и в область отрицательных абсцисс. То есть креатиффные господа сразу делят людей на положительных и отрицательных.
НМ ★★➦Andreiiiii• 29.12.24 23:34
Эээ... Я лучше промолчу. А то начну матом ругаться - Дима забанит.
На мой взгляд, вполне достаточно, что гауссиана не пересекает оси абсцисс. От слова "совсем".
Но вот интересно - если я, к примеру, ничего не понимаю в атомной физике или в морском деле, то я и ничего не пишу об этом.
Меня просто поражает при этом, как люди, не отличающие гауссиану от синусоиды, ухитряются писать о них обеих какие-то, б-дь, "глубокие мысли", на поверку оказывающиеся высосанным (хорошо еще, если из пальца) вычурным бредом недоучек с 4 классами ЦПШ? :-)
MarikaB➦Некто Леша• 30.12.24 02:46
Не ори. Криками ничего не изменишь - тут анонимная и безопасная среда общения:)
Читать надо не только матом... гауссиана ось абсцисс не пересекает. Но у нее есть значения и при положительных, и при отрицательных значениях оси абсцисс.
Леонид Хлыновский ★★★★★➦Andreiiiii• 30.12.24 09:35
Andreiiiii,
сделай мне скромный подарок на Новый год - поставь хоть один плюсик. Ну, или хотя бы не минусуй всё подряд.
А я за тебя Вернеру словечко замолвлю!
НМ ★★➦Andreiiiii• 30.12.24 10:28
Теоретически - да (если "сферический конь в вакууме").
Но практически (например, если мы изучаем распределение роста людей, или IQ, или числа эритроцитов в 1 мм3) - то в подавляющем числе случаев таки нет.
Так там и не гауссиана. А какой-нибудь Пуассон, биномиальное или что-нибудь позаковыристей.
Полная чушь. Распределение Гаусса применимо только в определенных условиях. Там где присутствует самовыборка (это когда люди решают участвовать или нет в эксперименте), там все предпосылки идут крахом.
"Мнение большинства - по определению ошибочно, потому что большинство людей, к сожалению, идиоты".
То, что все на свете распределено по Гауссу - это совершенно не так. Огромное количество величин в физике распределены иначе. Поэтому вот просто так на пустом месте утверждать про Гаусс для какой-то величины нельзя. Надо доказывать. К интеллекту это относится тоже.
Гаусс, вообще, возникает из центральной предельной теоремы, а она говорит о сумме случайных величин (в простейшем варианте независимых и одинаково распределенных, но есть много обобщений). То есть если что-то распределено по Гауссу, то там где-то внутри, скорее всего, прячется какой-то случайный аддитивный процесс. Например, если каждый человек каждый день зарабатыает случайное количество денег между 90 и 110 рублей, и никто ничего не тратит, то через год состояние всех людей будет хорошо описываться Гауссом. Если же процесс, например, мультипликативный, то никакого Гаусса не будет, хотя может по Гауссу распределиться логарифм величины.
На наличие какой-то суммы в вопросе человеческого интеллекта, вроде, ничего не указывает, поэтому Гаусса там ждать бессмысленно. Да это и интуитивно видно, все-таки, идиотов заметно больше, чем гениев.
Plato➦ystervark• 29.12.24 16:49
Да это и интуитивно видно, все-таки, идиотов заметно больше, чем гениев.
---------
Это просто генетическое нарушение (или приобретенное что реже), ну добавьте на него некую постоянную на левой стороне распределения. Кстати, в природе особи с серьезными нарушениями не выживают, так что в естественном виде без постороннего вмешательства ближе к Гауссу.
Ну и возможности мозга ограничены как по объему так и по скорости обработки информации, в отличие от пула суперкомпьютеров, так что некое предельное значение на правой стороне тоже есть.
людей гениальных, способных на прорыв в познании, чьи имена останутся в веках 0,5%
-------------
Звиздеж, 0,5% на 8 млрд., это значит имена 4 млн. из ныне живущих останутся в веках, не многовато ли "прорывов в познании"?
И да, самые успешные по жизни не обязательно из этих 0,5%, из верхнего квартиля вероятно, так и общайтесь с верхним квартилем, остальных в игнор, благо интернет это позволяет.
Дык вот и я про то же.
Причем в "справочнике" прямо так и написано :-)
Я комменты тогда ещё не читал. Дошёл до этого, проминусил и прокомментировал. Дальше читать не стал.
интересно происхождение этой записи в словаре. Ведь синусоиду все мы видели, ее в школе изучают. Кривая Гаусса на нее не похожа ну просто никак.
У нас в деревне тоже был аналогичный случай ... Мужик козе вдул и у неё рога поотпадали 🤣
"Если верить энциклопедическому словарю по психологии и педагогике, то Гауссиана: "нормальное распределение величин в виде синусоиды"
Сравнивать "гауссиану" с синусоидой - это как сравнивать треугольник с кругом. Ну, или как х... с пальцем, если уж совсем попросту.
https://ru.wikipedia.org/wiki/синусоида
https://ru.wikipedia.org/wiki/Нормальное_распределение
Короче, после столь бредового "зачина" - остальное можно вообще не читать.
Интересно, автор считает себя все же "интеллектуальной прослойкой", не умея даже прочитать в википедии про нормальное распределение?
Синусоиду автор ОБЯЗАН был изучать в 9 классе средней школы...
Тоесть"справочник Фонаревского"и"среднепотолочные цифры"-тут всё нормально?
Для 1%:этот текст-сплошной саркастический баян с идиоматической подспудностью смысла.
Ссылаться на викичто-то там-это в принципе прорыв!
Ептыть...
Этот текст на самом деле висит в "словаре": "Гауссиана распределение (или кривая)
- нормальное распределение величин в виде синусоиды"...
https://psychology_pedagogy.academic.ru/4465/Гауссиана_распределение_(или_кривая)
Воистину, "не дал Бог дороги - иди в педагоги", мать их за ногу...
Если мне пишут в первой строке "2х2=197,534" или "Саранск - столица штата Айова", я просто автоматически перестаю читать, т.к. за свои много лет не научился наслаждаться "сплошными саркастическими баянами с идиоматической подспудностью смысла" (что бы это не означало - лично я думаю, что это означает просто-напросто очередной несмешной п..деж).
Судя по числу минусов, я не одинок к такой оценке данного "идиоматической подспудности смысла" :-).
Не хотел наклоняться,но побежал глазами по строчкам имярека и решил сосредоточить
https://www.drive2.ru/b/526644630301706123/
Не иврит конечно,но что делать?
Зачем Вы вообще это еще раз скопировали? Я это уже пробежал взглядом, мне хватило одного раза.
Причем здесь иврит?
Вы хотите сказать, что для Вас любой, отличающий кривую нормального распределения от синусоиды, должен быть обязательно евреем?
Так я вас разочарую - я специалист в статистике, но не еврей.
Мои предки - крестьяне (потомки крепостных) с Тамбовщины и с Нижегородщины.
Обычно, когда говорят про гаусиану, имеют ввиду гладкость распределения. В этом смысле Гаус не отличается от Больцмана. В этом смысле я всегда плевался, когда мне говорили, будто распределение доли голосов на участках должно быть гаусовым. Но вообще, если взять синусоиду до пи, то разница с Гаусом будет заметная. Даже нарисовал из интереса.
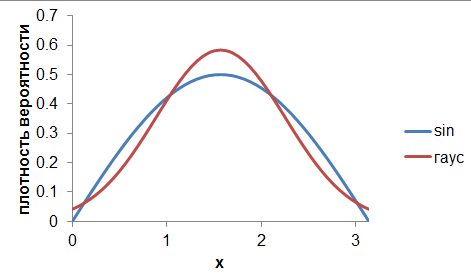
НМ ★★➦Kelavrik_0• 30.12.24 11:05
Ну, с неким приближением ту же Гауссиану можно попытаться аппроксимировать и треугольником ("пилой"), и полукругом, не говоря про биномиальное распределение, и т.п. Вопрос - а зачем?
Если вдруг возникнет какая-то задача в реальной жизни, гле кусок синусоиды будет описывать распределение чего-то ЛУЧШЕ, чем гауссиана - начнут использовать эту, блин, синусоиду.
Вон кто-то лет 15 назад показал, что распределение числа обострений неких заболеваний в год лучще всего описывается отрицательным биномиальным распределением - ну, мы все матюгнулись, проверили, согласились, и начали использовать negative binomial, мать его...
Ну да. Просто тут людям и не нужна точность. Их и синус устроит. Главное, чтоб купол был. И чтоб можно было отделить серёдку от краёв.
MarikaB➦Kelavrik_0• 30.12.24 02:51
не знаю, автор ли он, но он забыл или забил на роль системы образования. Каждое государство пропускает молодняк через это сито и приводит практически всех под один базовый уровень. Дальше как хотите - ебитесь раком или ебошьте в науку, но молодняк из школ выходит отформатированным под нужды правящего класса.