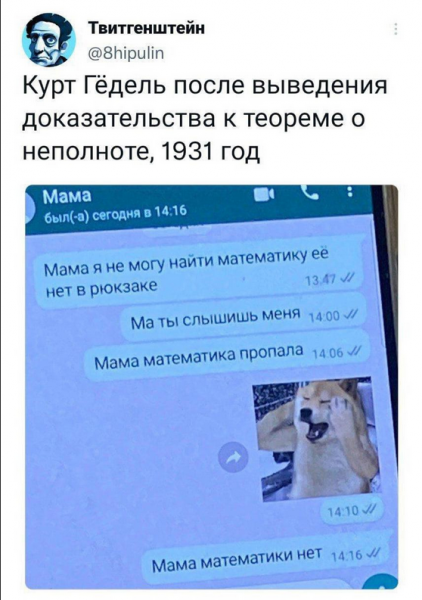
Математики не будет, Математики нет...
В теоремах Гёделя речь идёт о самоотрицающих утверждениях (парадоксы)

Вообще-то, в теореме Гёделя о неполноте ни слова не говорится о самоотрицающих утверждениях.
Гёдель доказал, что любая система аксиом либо противоречива - ну это понятно, что такое, либо неполна. Последнее означает, что в ней должны быть утверждения, которые в данной системе аксиом навозможно ни доказать, ни опровергнуть. Скорее всего, системы аксиом, которыми мы пользуемся (например, геометрия Евклида), неполны. И скорее всего, Лобачевский и вышел как раз на то утверждение (пятый постулат), которое невозможно ни доказать, ни опровергнуть с помощью остальных постулатов. И он же показал, как с этим бороться. Просто принимаем такое утверждение за очередную аксиому и развиваем систему дальше. Так что жива математика...
Математику найдешь,
Коль направо ты пойдешь.
Виден ориентир понятный -
Корень там растет квадратный..